こんにちは、実は数学大好きな篠原です。
数学って日常生活で使う機会もなければ、仕事にも使わない。だから数学は必要ないし、そもそも面白くない。
よく見聞きするワードです。
でもちょっと視野を広げると、実は数学が使える場所って意外なところにあるんです。
そこで今回の記事はまさかのHTML/CSSと数学の異色コラボになります。
なるべく難しい説明はしないように心がけたので、
数学が苦手or嫌いな方にも読んでいただけたら嬉しいです◎
nth-of-typeとは?
簡単に言うと、n番目の要素のスタイルを指定するためのものです。
直接何番目なのかを指定することもできれば、
奇数や偶数の場合はnth-of-type(odd)やnth-of-type(even)、
3の倍数の時はnth-of-type(3n)など、便利な指定をすることが出来ます。
参考:E:nth-of-type(n)-CSS3リファレンス
では、こんな時nth-of-typeをどうやって指定していますか?
こんな場合を考えてみます。
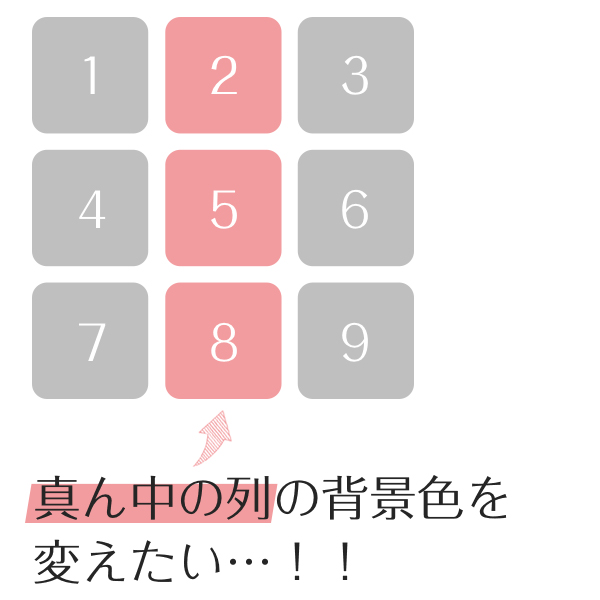
特定の列だけデザインを変えたい場面、結構ありますよね。
一見すると簡単そうに見えますが、よく見てみるとそうでもないことがわかります。
考えられるやり方としては、
①それぞれclassを付与する
②nth-of-type(2,5,8…)と指定する
などが主だと思います。
パッと見これでいいんじゃない?と思いますが、
レスポンシブでカラム数が変わった時や、アイテムの数が多かったりした時に
指定する数が多すぎる…などのデメリットが発生します。
これらのデメリットを全て解消してくれるのが「数列」の考え方です。
この考えを使うと、nth-of-type(3n)のように、nを使った指定をすることが可能になります。
数列とは?
“高校数学の数学2Bでやるやつ”です。
字の通り、数が列になったもので、例えば下記のようなものも数列となります。
1,2,3,4…(自然数を並べたもの)
1,3,5,7…(奇数を並べたもの)
2,4,6,8…(偶数を並べたもの)
数列として考えるとは?
今回やりたいことは、2番目、5番目、8番目、…のアイテムにcssを指定してあげるために、nを使ってnth-of-typeを指定するということです。
2,5,8,…という数列として考えた時に、下記の表のようになります。
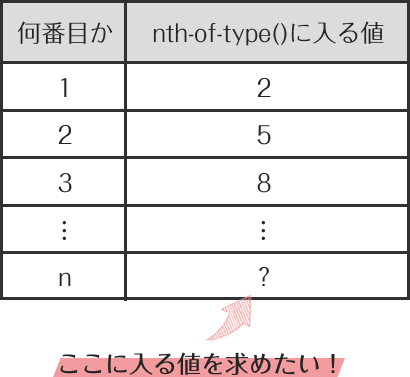
つまり、n番目に入る値を求めればよいということです。
これを数列の授業っぽく学校で習った言葉を使って言い換えると、その数列の「一般項」という言葉になります。
一般項が分かれば、たとえ10000個近くアイテムがあったとしても、nを使ったシンプルな式でnth-of-typeを指定することができます。
実際に2,5,8,…の数列のn番目(一般項)を求めてみよう
n番目の求め方というのはとてもシンプルで、以下の式で求められます。

a1というのは、初項、つまり数列の1番目の数字のことです。
dというのは、公差のことで、数がいくつずつ増えているのかということです。
2,5,8…の場合、3ずつ増えているのでd(公差)は3となります。
例:1,3,5,7…の場合、公差は2となります。
つまりa1 = 2, d = 3 なのでそれぞれあてはめていくと、
n番目 = 2 + 3(n – 1) = 2 + 3n – 3 = 3n – 1
つまり、nth-of-type(3n-1)と指定してあげればよいことになります。
このように、一見nth-of-typeで指定しにくいように見えるものも、
数列の知識を使うと簡単に指定してあげることができます。
これならわざわざclassを付与する必要もないですし、アイテムの数が膨大でも全てを指定せずに済みます。
※ただし、今回のやり方は、同じ数ずつ増えている数列にしか使えないので、注意してください。
まとめ
今回は、cssと数学という異色コラボの内容にしてみました。
授業っぽく言い換えると、今回の記事の数列の知識は「数列の初項と公差」「等差数列の一般項の求め方」みたいな感じです。
こんな時にも数学が役に立つのっておもしろいですよね。
日常生活で等差数列の一般項を求めることはそうそうないと思いますが、
実はかなり便利なので、ぜひ使えそうな時があれば使ってみてください!




